클레이튼 커쇼가 드디어 커리어 전성기를 맞이한듯 하다. 그는 6월 5일 현재까지 1.46의 ERA와 1.59의 FIP를 기록 중이다. 리그 평균값과 비교한 조정 평균자책점(ERA+)이 무려 260이나 된다. 이로 인해 요즘 계속 페드로 마르티네스의 전성기 시즌과 많은 비교가 되고 있다. 마르티네스는 2000년에 무려 291의 ERA+를 기록하였다.
그런데 우리는 ERA+로 서로 다른 시대의 평균자책점 가치를 정확히 설명할 수 있을까? 리그 평균과의 비교값이므로 어느정도는 맞다고 할 수 있다. 2000년 아메리칸리그는 평균자책점이 4.92점이며, 2016년 내셔널리그는 4.06점으로 거의 1점의 차이가 있으나, ERA+ 스탯은 이를 고려하고 있다. 그러나 일반적으로 평균이 낮아지면 평균값으로부터 벗어나기가 더욱 어려우며, 따라서 리그의 평균뿐 아니라 전체적인 분포의 형태까지 고려해야 더 정확하게 평가할 수 있다.
더욱이, 경기당 득점은 발생할 수 있는 최소값이 0점이지만 최대값에는 제한이 없다. 따라서 평균값(~4.5점)보다 훨씬 더 많은 득점이 발생하는 경기도 있으며, 이는 전체의 평균값을 높이게 된다. 결국 실제로는 평균보다 적은 득점이 발생하는 경기가 더 많은 셈이다.
그럼 이러한 득점 분포의 특징을 고려하여 평균자책점의 가치를 정확하게 평가하려면 어떻게 할까? 이전에 언급한 mERA+ 스탯을 다시 한번 자세히 살펴보자.
일반적으로 경기당 득점(x) 발생 확률은 베이불 분포(Weibull distribution)를 따르며, 함수의 식은 다음과 같다.
- p(x) = ( k / Lg_ERA ) x { ( x / Lg_ERA )^( k – 1 ) } x exp [ – { ( x / Lg_ERA )^k } ]
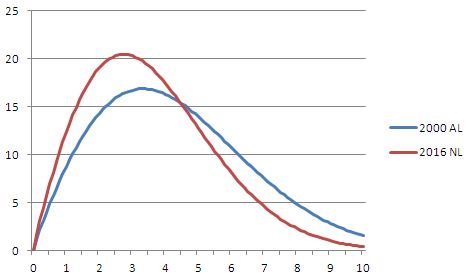
k는 분포의 모양을 결정하는 파라미터이며, Lg_ERA는 리그의 평균 ERA를 의미한다. 일반적으로 k는 1.9 수준으로 알려져 있다. 이제 이 함수를 이용하여 경기당 4.92점과 4.06점의 ERA 확률 분포를 살펴보자.
위의 분포에서 볼 수 있듯이, 기대 득점이 낮은 리그에서는 ERA 분포가 왼쪽으로 더 치우쳐 있으며, 평균값으로부터의 퍼짐 정도가 좀 덜 하다. 또한, 평균값보다 적은 득점이 발생할 확률이 더 높다는 것을 알 수 있다. 이는 앞서 말한 것처럼 많은 득점이 발생하는 경기가 전체 평균을 높였기 때문이다. 따라서 실제 리그 수준을 대표하기에는 평균값보다 중앙값(median)이 좀 더 적절하다. 리그 중앙값은 위의 와이블 분포 p(x)를 x에 대해서 적분한 값이 정확히 0.5가 되는 x의 값이다. 이를 계산하면 중앙값은 다음과 같다.
- median = Lg_ERA x ( log2 )^(1/k)
이 값은 특정 경기의 ERA가 더 낮거나, 더 높을 확률이 정확히 같은, 일종의 기준점이 된다. 이를 기준으로 하면 2000년 아메리칸리그는 4.06점, 2016년 내셔널리그는 3.35점이 얻어진다. 이제 다시 이 값을 기준으로 하여 투수의 ERA를 평가해보자.
투수의 ERA 분포 역시 장기적으로는 와이블 분포를 따른다고 가정할 수 있다. 그러면 투수가 이길 확률은 투수의 자책점이 리그 ERA 중앙값(median)보다 더 낮을 확률을 계산하면 된다. 투수의 ERA를 알 때, 평균자책점 분포는 다음과 같다.
- p(x) = ( k / ERA ) x { ( x / ERA )^( k – 1 ) } x exp [ – { ( x / ERA )^k } ]
이 때 투수가 x점보다 더 적은 자책점을 기록할 확률은 위의 확률 밀도 함수를 0부터 x까지 적분한 값(P(x))과 같다.
- P(x) = 1 – exp { – ( x / ERA )^k }
이제 이 식에 앞서 구한 리그 중앙값(median)을 대입하면, 투수가 리그 중앙값보다 더 적은 자책점을 기록할 확률(mERA+)을 계산할 수 있다.
- mERA+ = 1 – exp { – ( median / ERA )^k } x 100
- median = Lg_ERA x ( log2 )^(1/k)
mERA+는 리그 득점 수준을 정확하게 반영하고 있을 뿐 아니라 결과값의 범위도 0과 100사이로 제한되어 매우 실용적이다. 일반적으로 60점 이상이면 우수한 투수, 70점 이상이면 올스타 급의 투수, 80점 이상이면 사이영상 급의 투수라 해석할 수 있다. 90점 이상이면 역대급의 시즌이다.
그럼 이제 2000년 페드로 마르티네스와 2016년 클레이튼 커쇼의 mERA+를 계산해보자. k는 편의상 모두 1.9로 가정한다. 2000년 페드로 마르티네스의 ERA는 1.74이고, 리그 ERA 중앙값(median)은 4.06이므로 이를 대입하면 mERA+는 99.3이 얻어진다. 한편 2016년 클레이튼 커쇼는 1.46의 ERA와 3.35의 리그 중앙값을 대입하면 99.2가 된다. 마르티네스가 0.1점 더 높긴 하지만 이 정도면 사실상 거의 동등한 수준이다. 아직 시즌이 절반도 지나지 않은 상황이지만, 만일 커쇼가 지금의 페이스를 유지한다면 ERA 관점에서 커쇼의 2016년은 페드로 마르티네스의 2000년과 거의 동급이라 봐야겠다.
마지막으로 2016년 내셔널리그 투수 6월 5일까지의 mERA+를 살펴보자.
| Rank | Name | ERA | mERA+ |
| 1 | Clayton Kershaw | 1.46 | 99.2 |
| 2 | Jake Arrieta | 1.56 | 98.6 |
| 3 | Noah Syndergaard | 1.91 | 94.5 |
| 4 | Madison Bumgarner | 1.91 | 94.5 |
| 5 | Jason Hammel | 2.09 | 91.4 |
| 6 | Johnny Cueto | 2.16 | 90.0 |
| 7 | Drew Pomeranz | 2.22 | 88.8 |
| 8 | Jon Lester | 2.29 | 87.3 |
| 9 | Joe Ross | 2.37 | 85.5 |
| 10 | Jose Fernandez | 2.53 | 81.8 |
| 11 | Steven Matz | 2.60 | 80.2 |
| 12 | Jacob deGrom | 2.62 | 79.7 |
| 13 | Stephen Strasburg | 2.69 | 78.1 |
| 14 | Tanner Roark | 2.70 | 77.8 |
| 15 | Gerrit Cole | 2.72 | 77.4 |
| 16 | Kyle Hendricks | 2.84 | 74.6 |
| 17 | Jeff Samardzija | 2.84 | 74.6 |
| 18 | Kenta Maeda | 2.84 | 74.6 |
| 19 | Aaron Nola | 2.88 | 73.6 |
| 20 | John Lackey | 2.88 | 73.6 |