한국 최고 타자의 순위를 가리키는 말로, '추강대엽'이라는 말이 있다. '추신수 - 강정호 - 이대호 - 이승엽'을 의미하는 말이다. 특히, 상위 리그인 메이저리그에서 활약한 추신수와 강정호가 앞에 놓여 있다는 점이 인상적이다. 그런데 이들은 KBO, NPB, MLB 등 서로 활약한 리그가 다르기 때문에, 서로의 성과를 직접적으로 비교하기가 어렵다. 예를 들면 KBO에서의 50 WAR가 MLB에서의 5 WAR보다 가치가 있을까? ...
Category Archives: ETC
만장일치 MVP의 가치는 얼마나 더 클까?
2023년 오타니 쇼헤이와 로날드 아쿠냐 주니어가 각각 AL과 NL에서 만장일치로 MVP를 수상했다. 이렇게 양 리그에서 모두 만장일치 MVP가 나온 것은 역대 역대 최초이다. 그런데, 만장일치 MVP는 일반 MVP에 비해서 얼마나 가치가 더 높을까? 간단히, 만장일치 MVP 시즌과 만장일치가 아닌 MVP(일반 MVP) 시즌의 WAR를 비교해서 이를 확인해 보자. 역대 만장일치 MVP 수상자는 다음과 같다. YearLgNameTeambWAR1935ALHank GreenbergDET7.51936NLCarl HubbellNYG10.11953ALAl RosenCLE10.11956ALMickey ...
10년 동안 MVP를 가장 많이 배출한 팀
LA 에인절스는 2014년부터 2023년까지 최근 10년에, MVP를 무려 다섯 번이나 배출했다. 마이크 트라웃이 2014년, 2016년, 2019년에 AL MVP를 수상했고, 오타니 쇼헤이가 2021년과 2023년에 AL MVP를 수상했다. 평균적으로, 2년마다 한 번씩 에인절스 선수가 MVP를 수상한 셈이다. 굉장한 팀이다. 그런데 과거에도 이렇게 특정 기간에 MVP 수상자를 많이 배출한 팀이 있었을까? 10년 동안 MVP를 다섯 번 이상 배출한 팀은 ...
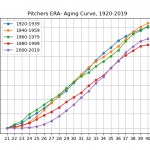
투수의 에이징 커브(aging curve)는 변하고 있을까?
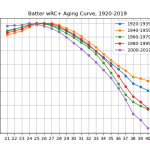
타자의 에이징 커브(aging curve)는 변하고 있을까?
로날드 아쿠냐 주니어의 인상적인 파워-스피드 넘버
로날드 아쿠냐 주니어가 2013년 8월 2일까지 32홈런-63도루를 기록 중이다. 이미, 역대 최초로 30홈런-60도루를 기록했고, 시즌 말까지 최소 30홈런-70도루, 또는 40홈런-80도루까지 가능할지 모른다. 물론, 그의 2023년보다 홈런이 많았던 시즌, 또는 도루가 많았던 시즌은 많았다. 그러나 이렇게 홈런과 도루를 동시에 많이 기록한 시즌은 흔하지 않다. 지금까지 40홈런-40도루 시즌은 다음과 같다. 1988년 호세 칸세코 (42홈런-40도루)1996년 배리 본즈 (42홈런-40도루)1998년 알렉스 로드리게스 ...
스티븐 스트라스버그와 앤서니 렌던, 누가 더 먹튀일까?
스티븐 스트라스버그와 앤서니 렌던, 둘 중 누가 더 먹튀일까? 두 선수는 모두 2019년 워싱턴 내셔널스의 우승 주역이다. 2020년부터 2026년까지 7년간, 총 2억 4500만불에 각각 워싱턴 내셔널스, 그리고 LA에인절스와 계약했다. 2020년 이후 스트라스버그의 WAR는 다음과 같다. 2020년: 0.02021년: 0.02022년: 0.0 팬그래프 기준, 이 성적의 가치를 금액으로 환산한 값은 다음과 같다. 1 WAR당 대략 8백만불로 계산한다. 2020년: $ 0.4M2021년: -$ 0.3M2022년: ...
메이저리그 역대 최고의 시즌은?
메이저리그 역대 최고의 시즌은 무엇일까? 베이브 루스의 1920년대, 배리 본즈의 2001-2004년, 페드로 마르티네스의 1999-2000년 등이 떠오른다. 그렇다면, 재미로 간단한 기준을 정해서 역대 최고의 시즌이 무엇인지 찾아보자. 물론 역대 최고의 시즌을 판단하는 기준은 주관적이다. 여기선 내가 생각하는 조건을 기준으로, 최대한 객관적이고 기계적으로 선택해 보자. 단, 1920년부터 2022년 시즌까지 만을 대상으로 한다. 그리고 조건은 다음과 같다. bWAR 그리고 fWAR ...
2023년 메이저리그 최고의 파워 히터(power hitter)와 파워 피처(power pitcher) 듀오는?
이전에 메이저리그 최고의 타자-투수 듀오를 살펴봤다. 간단히, 각 팀별로 wRC+가 가장 높은 타자와 ERA-가 가장 낮은 투수를 선정하여, 팀 최고 타자의 wRC+에서 팀 최고 투수의 ERA-를 뺀 값으로 계산하였다. 이번에는 이와 유사하게, 최고의 파워 히터(power hitter)와 파워 피처(power pitcher) 듀오를 알아보자. wRC+와 ERA-와 달리, 이번엔 타자의 홈런과, 투수의 탈삼진을 기준으로 한다. wRC+와 ERA-보다 더 직관적이고 이해가 쉽다. 또, ...
마이크 트라웃의 실력은 하락한 적이 있었나?
마이크 트라웃은 2023년에도 뛰어난 활약을 보이고 있다. 4월 25일까지 .326/ .426/ .605, 5 HR, 186 wRC+라는 MVP 급의 성적을 기록 중이다. 30세 이후에도 여전히 최고의 기량을 유지하는 것이 놀랍다. 그런데 그의 실력은 지금까지 하락한 적이 없었던 걸까? 물론 그는 성적이 하락한 적이 여러 번 있었다. 2014년에 풀 시즌을 소화하고도 처음으로 10 WAR 이하의 성적을 기록하였고, 2017년엔 ...
메이저리그에서 가장 재미있는 선수(most fun player)는 누구일까?
메이저리그에서 팬들에게 가장 큰 즐거움을 주는 타자는 누구일까? 이전에 이와 유사하게, 익사이팅 플레이어(exciting player)를 확인한 적이 있다. 이를 위해, 익사이팅 스코어(EXCT)를 정의했는데, 선수의 승리 기여도(WAR)에서 볼넷으로 인한 기여도를 빼고, 도루 실패로 손실된 기여도를 다시 보상했다. 수식은 다음과 같다. EXCT = WAR + 0.03 × (CS – BB) EXCT는 WAR보다 팬들이 느끼는 즐거움을 더 잘 설명한다. 다만, EXCT는 여전히 팬들이 ...
MVP(Most Valuable Player)와 MOP(Most Outstanding Player)
2022년 9월 30일까지, 애런 저지의 활약은 역대급이다. 단지 61개의 홈런을 친 것을 넘어서, .313/.425/.696, 209 wRC+, WAR 11.0의 역대급 성적을 기록 중이다. 역대 최고의 타자 시즌 중 하나로 간주될 만하다. 당연히 가장 강력한 AL MVP 후보이다. 한편, 이와 비견될 만한 선수가 있다. 오타니 쇼헤이는 2022년 9월 30일까지, 지명타자로서 .275/.358/.529, 145 wRC+, WAR 3.9의 성적을, 동시에 선발투수로서 ...
야구의 꽃 – 홈런, 도루, 삼진 – 을 많이 기록한 시즌
타자가 타석에서 할 수 있는 가장 좋은 것은 역시 '홈런'이다. 주자로서는 '도루'가 대표적이다. 반면, 투수로서는 '삼진'을 잡는 것이다. 즉, '홈런', '도루', '삼진'은 각각 타자, 주자, 투수로서 기록할 수 있는 대표적인 야구 스탯이다. 그야말로 '야구의 꽃'이라 할 수 있다. 1920년 이후 홈런을 가장 많이 친 타자의 시즌은 다음과 같다. RankNameSeasonHR1Barry Bonds2001732Mark McGwire1998703Sammy Sosa1998664Mark McGwire1999655Sammy Sosa2001646Sammy Sosa1999637Roger Maris1961618Babe Ruth1927609Giancarlo ...
홈런은 많고 병살타는 적은 타자들
타자가 타석에서 할 수 있는 가장 좋은 것은 무엇일까? 바로 홈런을 치는 것이다. 혹자는 홈런보다 나은 안타가 있다고도 하지만, 그런 건 없다. 홈런이 가장 좋다. 홈런은 평균적으로 대략 기대 득점을 1.4점 높인다. 그럼 최악의 상황은 무엇일까? 바로 병살타를 치는 것이다. 물론 트리플 플레이가 더 나쁘지만, 이는 상당히 드물다. 일반적으로, 병살타를 치는 것은 타석에서의 최악의 성과라고 할 ...
애런 저지는 2022년에 60홈런을 기록할 수 있을까?
애런 저지는 2022년 7월 2일까지 .286/ .361 /.627, 175 wRC+, 4.0 WAR의 놀라운 성적을 기록 중이다. 특히, 전반기가 아직 끝나지도 않은 시점에서 무려 홈런이 29개이다. 그렇다면 그는 2022년에 최종 60홈런을 기록할 수 있을까? 한 시즌 60홈런은 도대체 얼마나 어려울까? 2000년 이후 60홈런을 기록한 시즌은 단 두 번이다. 2001년의 배리 본즈(73개)와 새미 소사(64개)가 전부이다. 그나마 그 ...